怎么解包含两个变量的代数方程组(方程组2的解都是方程组1的解)

网友陈韵伟提问：

如何解包含两个变量的代数方程组(方程组2的解都是方程组1的解)

方程组问题将要求您同时解决两个或两个以上的方程。当有两个不同的变量时，如x和y，或a和b，乍一看，你可能会觉得题目很难。幸运的是，在知道了方法之后，你只需要使用基本的代数技能，偶尔使用一点分数知识来解决问题。假如你是视觉学习者，或者你的老师提出要求，那么你也可以学会画方程式。绘图对了解情况或检查自己的解题过程非常有用，但可能比其他方法慢一点，不适合所有方程组。

方法1方法1 的 3:使用代入法

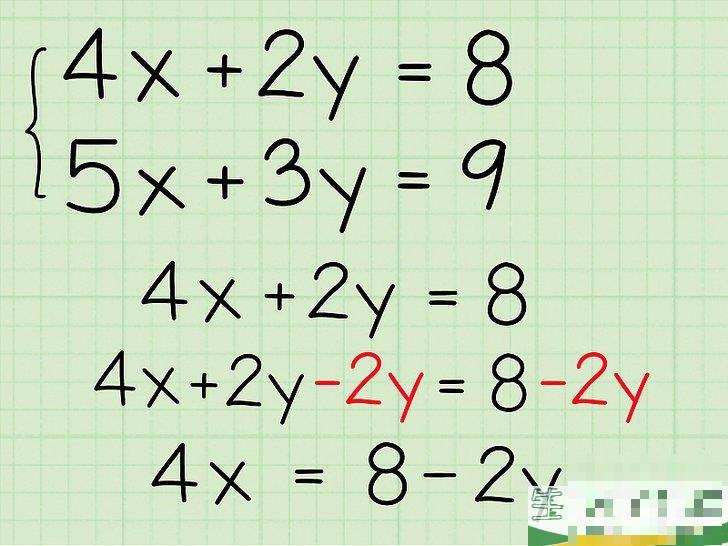
将变量分别移到方程的两侧。

在使用这种替换方法时，首先需要使用其中一个方程解决x或者任何其他变量。例如，假设主题中的方程是

4x 2y = 8

和

5x 3y = 9

。先看第一个方程。方程变形，两侧减去2y，得到：

4x = 8 - 2y

。通常在这种方法之后使用分数。假如你不喜欢分数，试试下面介绍的消元法。

解决方程两侧的除法x”。

当方程的一侧变量出现在方程的一侧时，双方同时进行除法，以获得变量本身。

4x = 8 - 2y

(4x)/4 = (8/4) - (2y/4)

x = 2 - ?y

将其代入另一个方程。

一定要代入一个

方程，而不是你已经使用过的方程。替换解决的变量后，方程只剩下一个变量。例如：已知

x = 2 - ?y

。

没有任何变化的第二个方程是

5x 3y = 9

。

在第二个方程中使用2 - ?y”代替x：

5(2 - ?y) 3y = 9

。

解决剩余变量。

现在，你得到一个只有单个变量的方程。使用普通代数法来解决这个变量。

如果变量被抵消，跳到最后一步。

在其他情况下，您将获得变量解：

5(2 - ?y) 3y = 9

10 – (5/2)y 3y = 9

10 – (5/2)y (6/2)y = 9

，如果不了解这一步的计算过程，可以学习分数加法。这种方法经常使用这部分知识，但并不总是如此。

10 ?y = 9

?y = -1

y = -2

用答案来解决另一个变量。

不要只犯一半的错误来解决问题。您需要将答案代入一个原始方程来解决另一个变量：已知

y = -2

原始方程之一是

4x 2y = 8

。这一步可以使用两个方程中的任何一个。

用-2代替y：

4x 2(-2) = 8

。

4x - 4 = 8

4x = 12

x = 3

当两个变量都被抵消时，知道该怎么办。

将

x=3y 2

或者当类似的答案被替换为另一个方程时，要一个只有单个变量的方程。但有时候，你会得到一个没有

变量方程。仔细检查解决问题的过程，确保您将变形方程替换为方程中，而不是返回方程一。如果你确信你没有犯任何错误，你的结果应该属于以下情况之一：如果你得到的方程没有变量或等式，例如3 = 5，则问题

无解

。如果你画两个方程，你会发现它们是平行的，永远不会相交。

如果你得到一个等式建立

无变量方程，如3 = 3，则问题有

无穷多解

。方程组中的两个方程完全相等。如果你画它们的图形，你会发现它们是同一条直线。

广告

方法2方法2 的 三、使用消元法

找到可抵消的变量。

有时候，当两个方程加起来时，会有一个可以抵消的变量。例如，方程

3x 2y = 11

和

5x - 2y = 13

相加时，“ 2y”和“-2y相互抵消，消除方程中的所有‘’y项目。观察主题中的方程，看看是否有一个这样抵消的变量。如果没有，请参考下一步的建议。

乘法一对一方程，使变量可以抵消。

如果变量已经被抵消，请跳过如何解决包含两个变量的代数方程组的方法。如果两个方程中没有可以自然抵消的变量，你可以变形其中一个方程来抵消变量。为了理解，让我们举一个例子：你有一个方程组：

3x - y = 3

和

-x 2y = 4

。

首先，变形的第一个方程，让变量

y

也可以选择抵消。

x

，答案是一样的。

在第一个方程中

- y

必须和第二个方程

2y

抵消。你可以用2乘以

- y

，实现这一目标。

同时乘以第一方程的两侧，

2(3x - y)=2(3)

，得到

6x - 2y = 6

。这样一来，

- 2y

在第二个方程中

2y

抵消。

三把两个方程加起来。

当两个方程加起来时，用左边和左边加起来，用右边和右边加起来。如果以正确的方式变形方程，应抵消其中一个变量。以上一步的方程组为例:两个方程是

6x - 2y = 6

和

-x 2y = 4

。

左侧相加得到：

6x - 2y - x 2y =??

右侧加得到：

6x - 2y - x 2y = 6 4

。

四解最终变量。

简化相加得到的方程，然后用基本代数解决最终变量。

如果简化后方程没有变量，可以直接跳到本节的最后一步。

在其他情况下，你应该能够得到一个简单的变量解决方案。例如：你得到了

6x - 2y - x 2y = 6 4

。

将

x

变量和

y

变量分类排序：

6x - x - 2y 2y = 6 4

。

简化得到：

5x = 10

解x：

(5x)/5 = 10/5

，所以

x = 2

。

5解决另一个变量。

你已经找到了一个变量，但问题还没有解决。将答案代入原始方程，解决另一个变量。例如：已知

x = 2

，其中一个原始方程是

3x - y = 3

。

用2代替x：

3(2) - y = 3

解方程中的y：

6 - y = 3

6 - y y = 3 y

，所以

6 = 3 y

3 = y

当两个变量都被抵消时，知道该怎么办。

有时，两个方程加起来会得到一个毫无意义的方程，或者至少对解决问题没有帮助。从头开始，仔细检查你的解决问题的过程，但如果你确信你没有犯错误，你可以根据以下情况中的一个写下答案：如果添加方程没有变量，等式不成立，例如2 = 7，则方程组

无解

。如果你画两个方程，你会发现它们是平行的，永远不会相交。

如果添加后的方程没有变量，并且设置了等式，则方程组有

无穷多解

。两个方程实际上是一样的。如果你画它们的图形，你会发现它们是同一条直线。

广告

方法3方法3 的 三、画方程图

1只在有要求时使用这种方法。

除非使用计算机或图形计算器，否则解决方程组通常只能得到类似的答案。老师或数学教科书可能会要求你使用这种方法来熟悉如何将方程画成直线。你也可以用这种方法来检查其他方法的答案。该方法的基本思路是绘制两个方程的图形，并找到它们的交点。此点的x和y是方程组的x和y。

解两个方程y。

保持两个方程的独立性，并使用代数方法将其变成y = __x __例如：第一个方程是

2x y = 5

。把它变成

y = -2x 5

。

第二个方程是

-3x 6y = 0

。把它变成

6y = 3x 0

，然后简化成

y = ?x 0

。

若两个方程相同

，两条直线将完全重叠。你可以写方程组

无穷多解

。

3画坐标轴。

在坐标纸上画一个垂直的y轴”和一条水平的“x轴。从它们的交点开始，沿y轴向标记一、二、三、四等数字，然后沿x轴向右做同样的事情。沿y轴向下，x轴向左标记-1、-2等数字。如果没有坐标纸，可以用尺子保证每个数字之间的间距相等。

如果使用较大的数字或小数字，您可能需要以不同的方式调整图形比例。例如，将原始的1、2、3点标记为10、20、30或0.1、0.2、 0.3。

画出每条线的y轴截距。

将方程变形成

y = __x __

在形式之后，你可以开始绘制它的图形，首先绘制直线和y轴之间的点。这个点在y轴上的值必须等于方程最后的数字。在之前的例子中，第一条直线(

y = -2x 5

)与y轴在

5

这一点相交。另一个方程(

y = ?x 0

)的直线则在

0

这一点相交。它们对应图形中的(0,5)和(0,0)。

如果可以的话，你应该用不同颜色的笔画两条直线。

继续用斜率画直线。

在

y = __x __

在形式方程中，x前面的数字是直线斜率

。x值每增加1时，y值的增量等于斜率。利用这一规律在图形中绘制x=1点，两条直线上的点。你也可以把它们放在一边x = 1代入两个方程，找出y的值。在这个例子中，直线

y = -2x 5

的斜率为

-2

。当x = 1时，直线会从x = 0的位置向下

移动两个单位。画出(0,5)和(1,3)之间的线段。

直线

y = ?x 0

的斜率是

?

。当x = 1时，直线会从x = 0的位置向上

移动单位。画出(0，0)和(1，)之间的线段。

如果两条直线有相同的斜率

，所以它们永远不会相交，所以方程组没有解决办法。你可以写下来

无解

二字。

在它们相交之前，延长两条直线。

停下来观察图形。如果两条直线已经相交，则跳到下一步。否则，你应该根据直线的情况作出决定：如果两条直线互相靠拢，那么你应该继续在这个方向上画更多的点。

如果两条直线相距越来越远，你应该从x = -一开始，向另一边画更多的点。

如果两条直线相距较远，试着画出更远的点，比如x = 10那一点。

7在交点找到答案。

两条直线相交后，交点的x值和y值是问题的答案。幸运的是，答案将是整数。例如，在这个例子中，两条直线在点

(2,1)

相交，所以答案是

x = 2和y = 1

。在某些方程组中，直线交叉值在两个整数之间，除非图形非常准确，否则很难判断它的具体位置。在这种情况下，你可以直接写下答案，比如x在1到2之间，或使用替代法或消元法来获得准确的答案。

注意事项

您可以将答案代回原始方程，检查您的解决过程是否正确。如果代入后，方程等式成立，如3 = 三、答案正确。

为了消除变量，有时需要使用负数乘以方程。

广告

警告

这些方法不适用于二次或二次以上的方程，如包含x的方程。如果您想了解更多关于此类方程的信息，可以参考二元二次方程因式分解的文章。

广告

jiaoyu/11893.html

以上就是方程,变量,方程组的相关信息信息，希望对你有所帮助。

以上就是的相关信息资料了，希望能帮到您。