怎么求两个数的最小公倍数(怎么求两个数的最小公倍数短除法)

感谢百宜网友提问：

如何获得两个数的最小公倍数(如何获得两个数的最小公倍数的短除法)

倍数是数乘以整数的结果。一组数字的最小公倍数(简称LCM）它是这组共有倍数中最小的。要找出最小公倍数，您需要首先确定每个数字的因数。解决最小公倍数的方法有很多。本文介绍的方法适用于寻找两个或两个以上数字的最小公倍数。

方法1方法1 的 4:列出数字的所有倍数

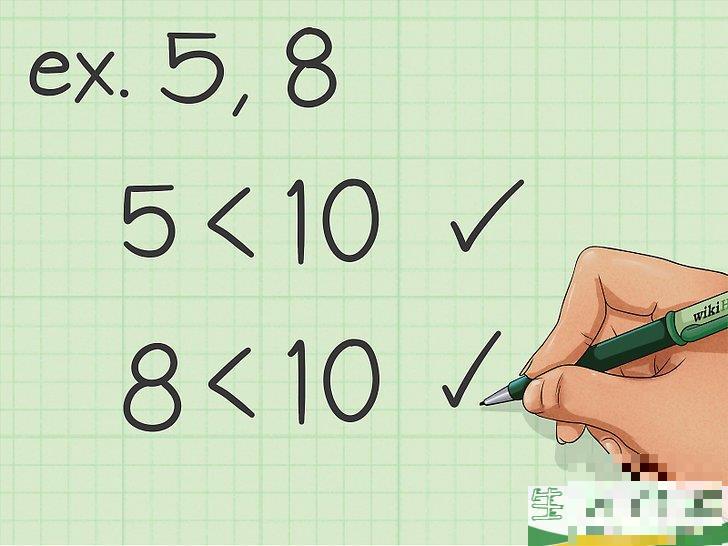
评估你要计算的数字。

这种方法最适合计算两个小于10的数字的公倍数。如果你面对的是更大或更多的数字，最好使用其他方法。例如，我们需要找到5和8的最小公倍数。由于这两个数字都相对较小，因此适合使用这种方法来获得它们的最小公倍数。

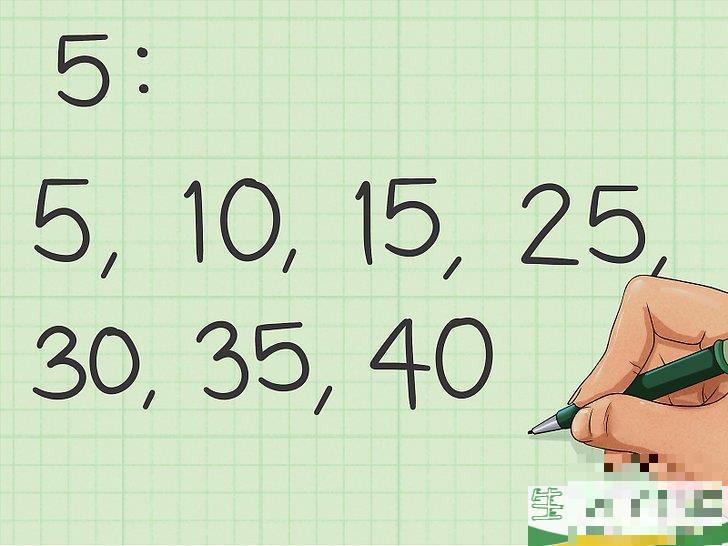
从小到大列出第一个数字的几个倍数。

用第一个数字乘以不同的整数来获得它的倍数。换句话说，你可以直接查看乘法表，找到一个数字的倍数。例如，第一个数字5的倍数为5、10、15、20、25、30、35和40。

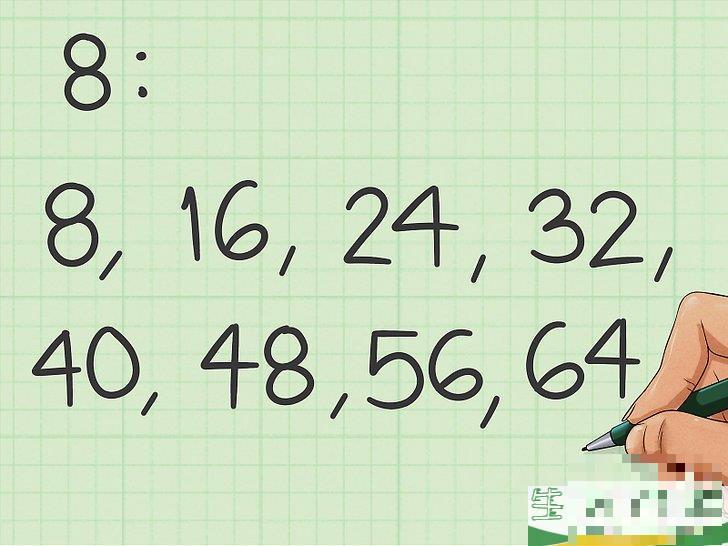
从小到大写下第二个数字的几个倍数。

将相同的整数乘以第二个数字，得到几个倍数，与之前的一组倍数进行比较。在我们的例子中，数为8、16、24、32、40、48、56和64。

比较两个数字的倍数，找到最小的相同倍数。

你可能需要列出更多的倍数来找到相同的倍数。你能找到的最小相同的数字是最小的公倍数。例如，5和8的倍数中有40，而且它是最小的相同倍数，所以40是5和8的最小公倍数。

广告

方法2方法2 的 4:使用因素分解法

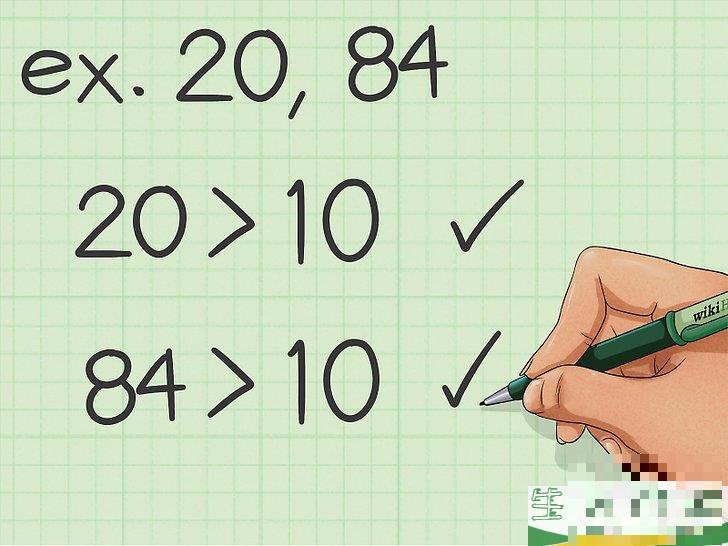
1评估数字。

这个方法最适用于计算两个大于10的数字的公倍数，如果你面对的是比较小的数字，最好使用其它方法快速求出最小公倍数。例如，如果你要找出数字20和84的最小公倍数，你可以使用这种方法。

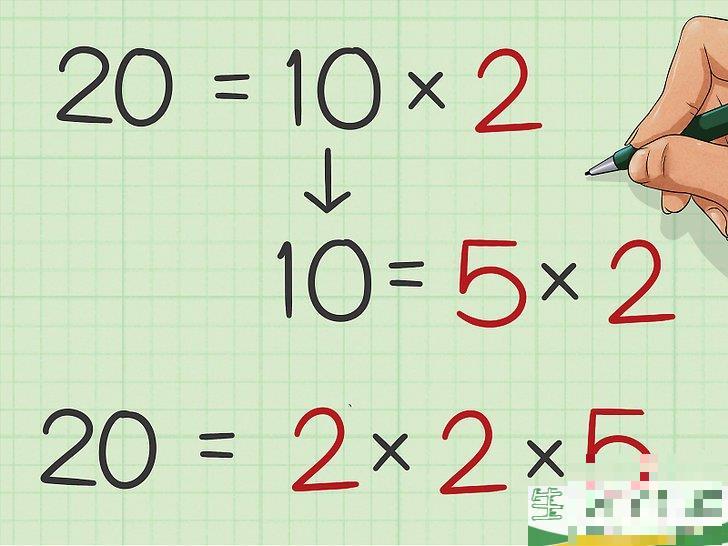
因式分解第一个数字。

你可以把第一个数字因子分解成它的素数因数，乘以几个素数因数，你可以得到原始数字。您可以绘制因子树来将数字分解为素数。在完成因子分解后，重写等式。等式的一边是分解的数字，另一边是素数因数。 2

×

10

=

20

{\displaystyle \mathbf {2} \times 10=20}

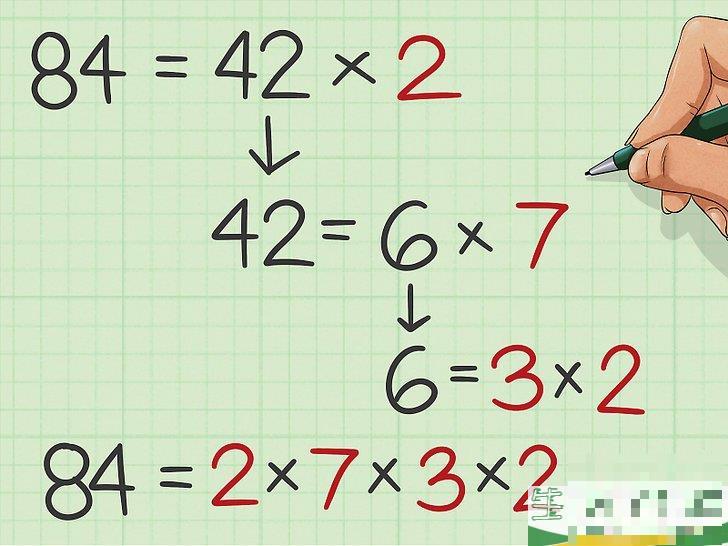
第二个数字也因式分解。

以相同的方式分解第二个数字，找到其素数因数，并乘以每个素数因数获得第二个数字。 2

×

42

=

84

{\displaystyle \mathbf {2} \times 42=84}

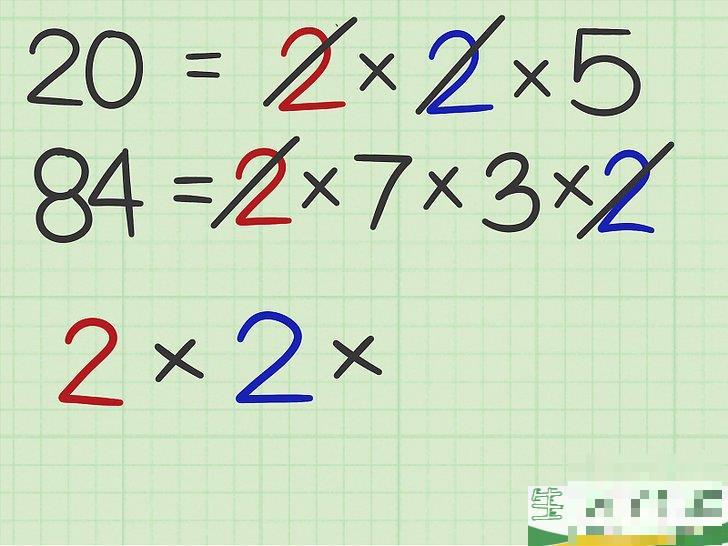
写下每个相同的素数因数，并将每个因数相乘，写成乘法等式。

当您写下每个因数时，请在因式分解等式中划掉相应的值。例如，这两个数字有共同的因数2，因此，写下因数 2

×

{\displaystyle 2\times }

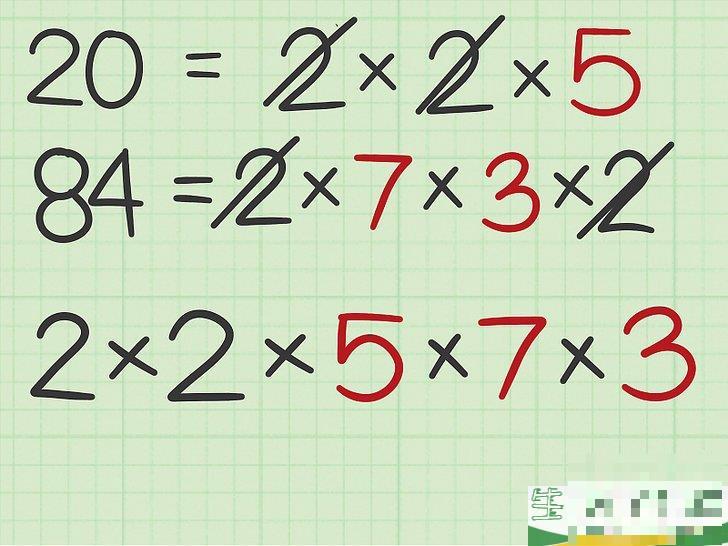
将剩余因数添加到乘法子中。

剩余因数是指在划掉公因数后，几个因式分解的等式中没有划掉的因数。也就是说，这两个数字的因数是不同的。例如，在等式 20

=

2

×

2

×

5

{\displaystyle 20=2\times 2\times 5}

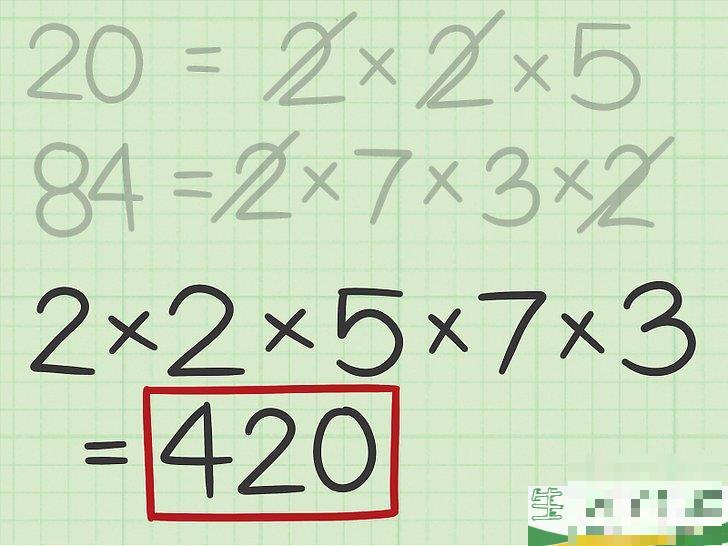
计算最小公倍数。

乘以上述所有因数，得到最小公倍数。在我们的例子中， 2

×

2

×

5

×

7

×

3

=

420

{\displaystyle 2\times 2\times 5\times 7\times 3=420}

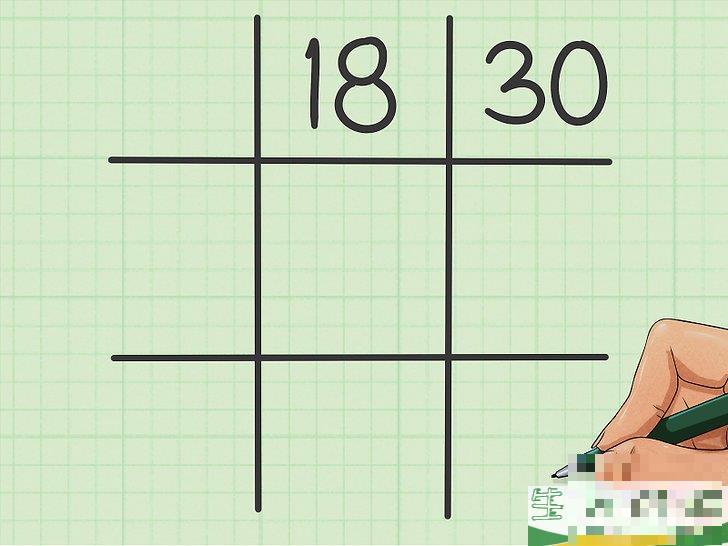
1画井形网格。

井形网格由两组平行线交叉组成，两组平行线相互垂直，形成三行三列网格，看起来像手机或键盘上的井字键(#)。第一个数字写在网格顶部中央的方格内，第二个数字写在网格右上角的方格内。例如，如果您想找到数字18和30的最小公倍数，请将18写在顶部中央的方格中，并在网格右上角的方格中写下30。

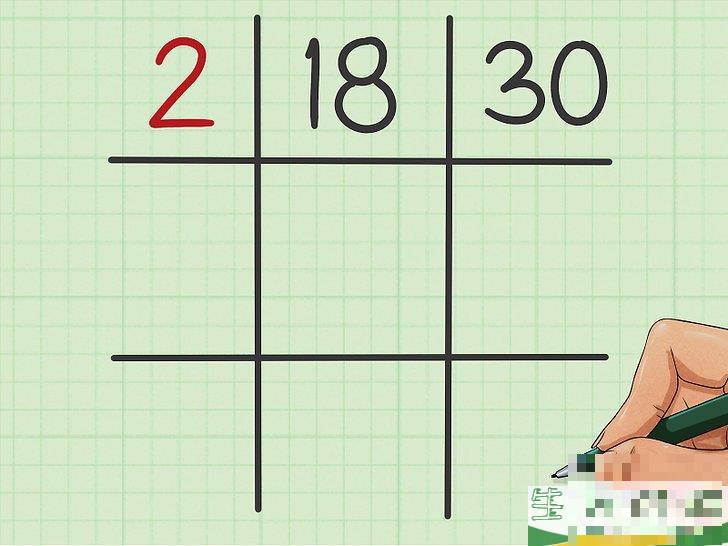
找出两个数字共有的因数。

将这个数字写在网格左上角的方格中。最好使用素数因数，这将极大地促进后续计算，但不必要。在解决18和30的最小公倍数例中，由于18和30是偶数，因此可以将2删除并写在网格左上角的方格中。

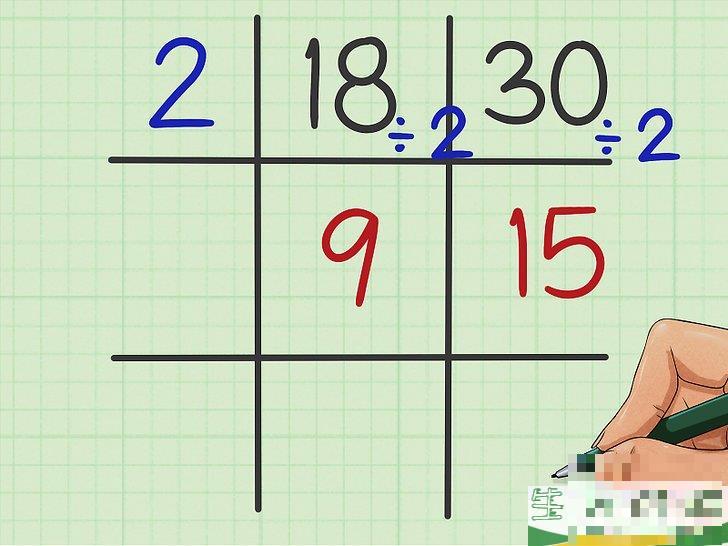
用例题中的两个数除以共同因数。

将除得的商写在每个数字下面的方格中。进行除法计算就能得到商。例如，18

÷

2

=

9

{\displaystyle 18\div 2=9}

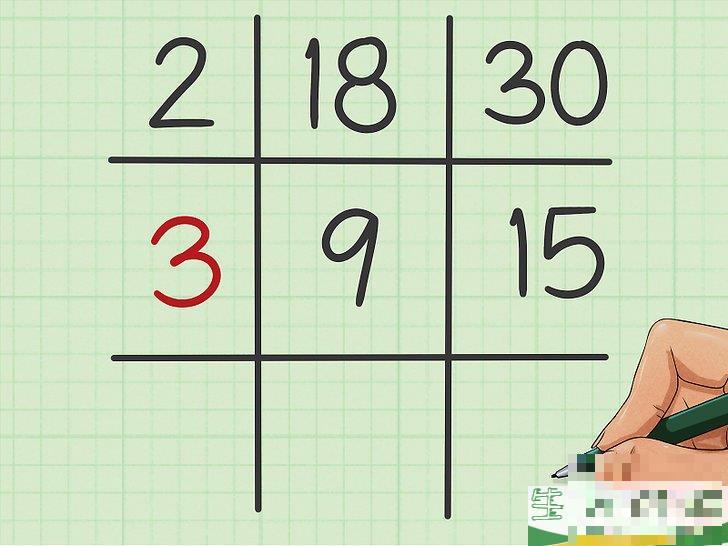
找出两个商家的公因数。

如果两个业务没有公共因素，你可以跳过这一步直接进入下一步。如果它们有公共因素，请写在网格中心左侧的网格中。例如，9和15的公共因素是3，所以在网格中心左侧的网格中写3。

5用第一步得到的商除以新的公因数。

在上一步的结果下写下结果。 9

÷

3

=

3

{\displaystyle 9\div 3=3}

如有必要，继续扩展井字网格，画得更大。

然后按照上述两个数的最小公倍数计算除法，直到两个业务没有相同的因数。

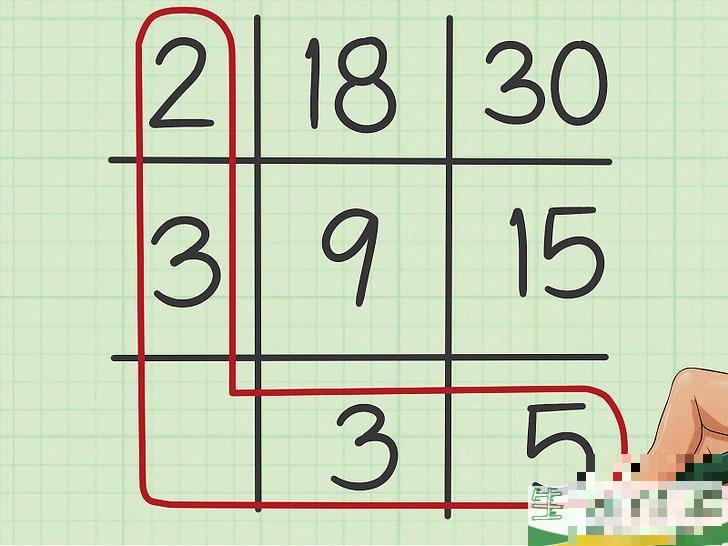
7在网格第一列和最后一行的数字上画圈。

圆圈连在一起，就像画一幅大写L字母。乘以圈出的所有数字。在我们的例子中，2和3位于网格的第一列，3和5位于网格的最后一行，写出数学风格: 2

×

3

×

3

×

5

{\displaystyle 2\times 3\times 3\times 5}

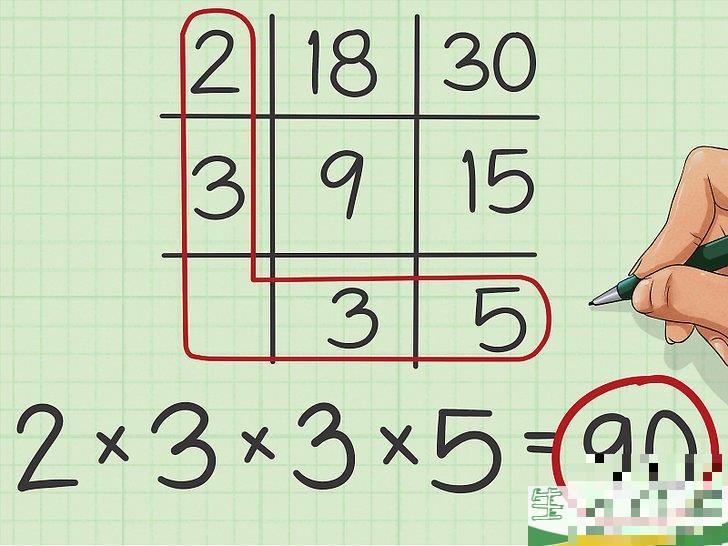
完成乘法计算。

乘以所有因数，结果是原两数的最小公倍数。 2

×

3

×

3

×

5

=

90

{\displaystyle 2\times 3\times 3\times 5=90}

解除法中的名词。

除数是除法操作中被另一个数除以的数字；除数是除数除以的数字；业务是除法的最终结果；余数是整数除以后剩余的数字。例如，在方程15中

÷

6

=

2

余

3

{\displaystyle 15\div 6=2\;{\text{余}}\;3}

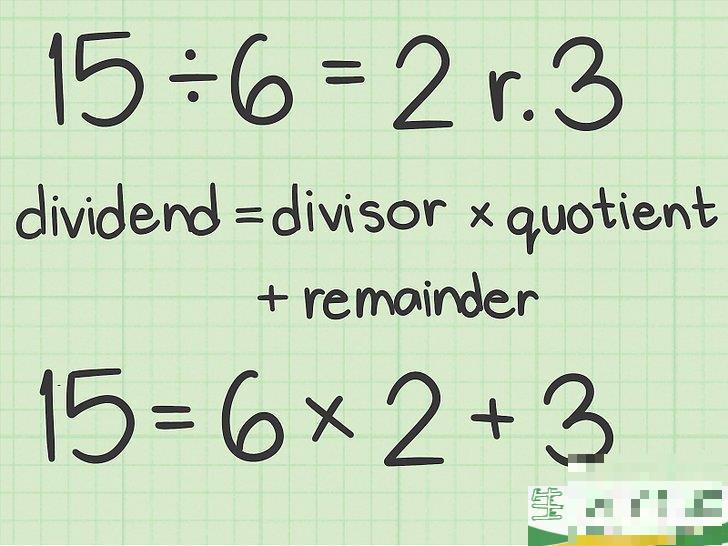
将方程改写为商-余数。

公式是

被除数 = 除数 × 商 余数

。根据欧几里得算法，你需要用这个公式找出两个数字的最大公约数。例如，15

=

6

×

2

3

{\displaystyle 15=6\times 2 3}

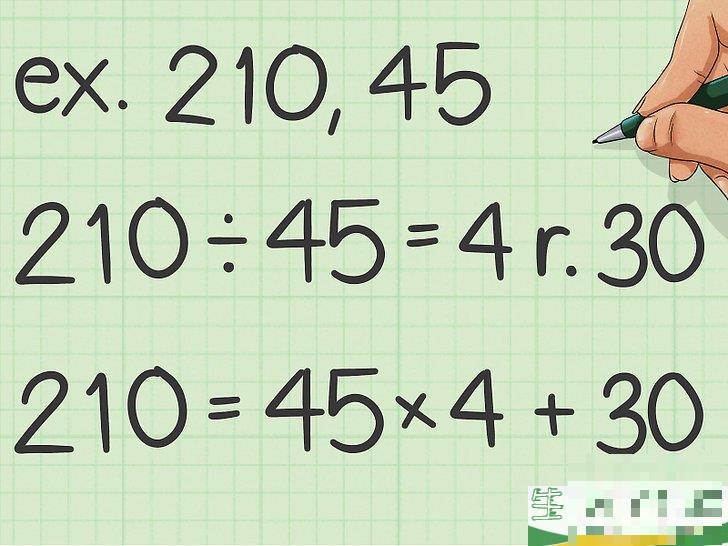
用两个数字中较大的数字作为除数，用较小的作为除数。

建立两个数字的商-余数方程。例如，如果您需要210和45的最小公倍数，则方程的形式是 210

=

45

×

4

30

{\displaystyle 210=45\times 4 30}

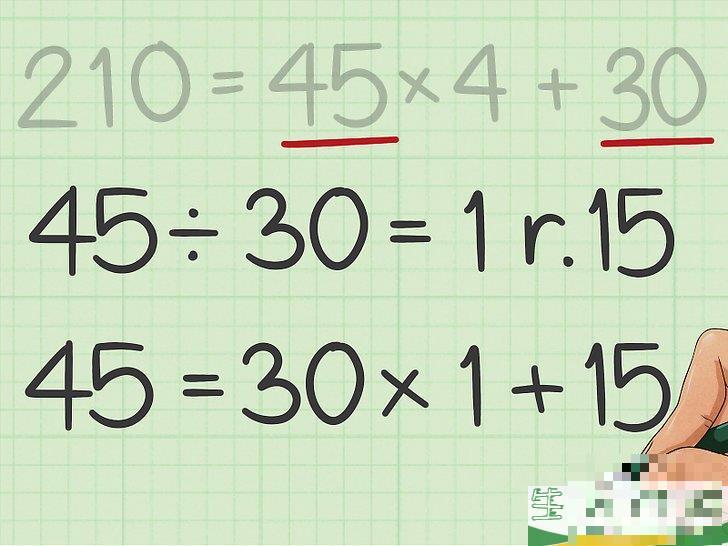
4用原除数作为新的被除数，用余数作为新的被除数。

建立两个数字的商-余数方程。 45

=

30

×

2

15

{\displaystyle 45=30\times 2 15}

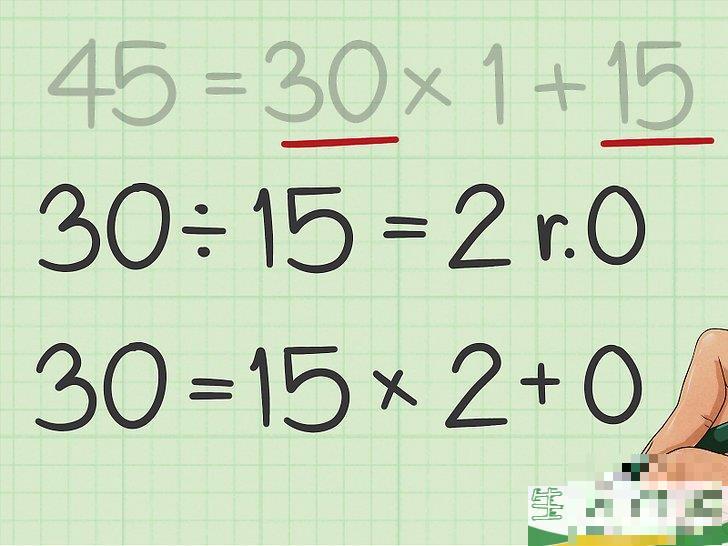
重复这个过程，直到最后的余数变成0。

在每个新方程中，您需要使用原除数作为新的被除数，并使用余数作为新的被除数。例如，30

=

15

×

2

{\displaystyle 30=15\times 2 0}

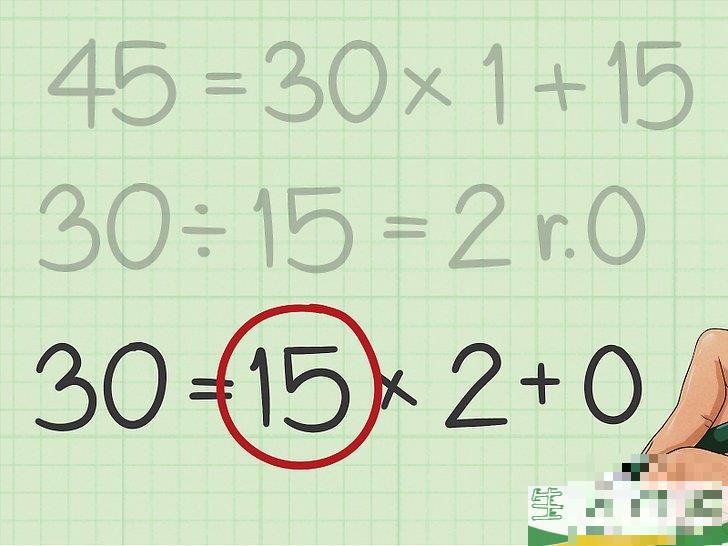
在最后一个方程中找到除数。

这个数字是两个数字的最大公约数。例如，最后一个方程30

=

15

×

2

{\displaystyle 30=15\times 2 0}

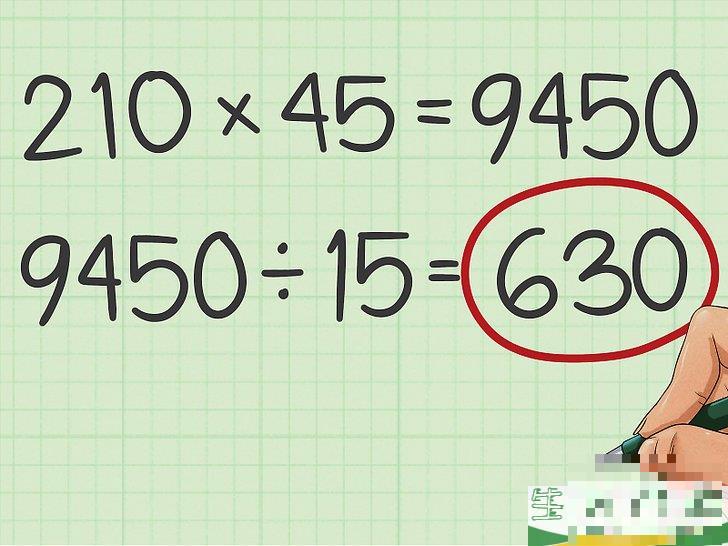
7找出两个数字的乘积。

用它们的乘积除以它们的最大公约数。最终结果是两个数字的最小公倍数。例如，210

×

45

=

9450

{\displaystyle 210\times 45=9450}

。乘积除以最大公约数，得到9450

15

=

630

{\displaystyle {\frac {9450}{15}}=630}

。因此，630是210和45的最小公倍数。

广告

注意事项

如果您需要多个数字的最小公倍数，则需要稍微更改上述方法。例如，要找到16、20和32的最小公倍数，请使用上述方法找到16和20的最小公倍数（80）。然后找到80和32的最小公倍数，最终计算结果为160。

最小公倍数有很多用途。最常见的用途是，当你计算分数的加减法时，几个分数的分母数必须相同；如果分母不同，你需要将分子和分母乘以一个数字，使几个分数的分母变成相同的数字。最好的办法是找到最小公分母（LCD），也就是说，分母的最小公倍数（LCM）。

广告

jiaoyu/11902.html

以上就是最小公倍数,数字,两个的相关信息资料了，希望能帮到您。

以上是相关信息，希望对您有所帮助。