怎么求3X3矩阵的行列式(3x1的矩阵行列式怎么算)

王哲豪网友提问：

怎么求3X3矩阵的行列式

权威答案：

矩阵的行列式常用于微积分、线性代数和高等几何。求一个矩阵的行列式一开始可能会让人困惑，但只要做过几次后，你就会觉得并不是那么难。

方法1方法1 的 2:求行列式

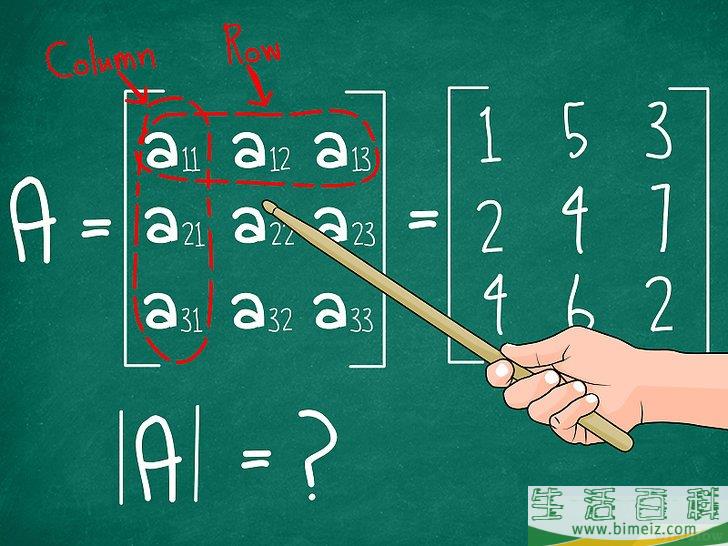
1写出3×3矩阵。

我们从3x3矩阵A开始，试着找出它的行列式|A|。下面是我们将使用的一般矩阵表示法，以及示例矩阵：M

=

(

a

11

a

12

a

13

a

21

a

22

a

23

a

31

a

32

a

33

)

=

(

1

5

3

2

4

7

4

6

2

)

{\displaystyle M={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}={\begin{pmatrix}1&5&3\\2&4&7\\4&6&2\end{pmatrix}}}

2选择单行或单列。

这将是引用行或列。不管你选哪一行或列，结果都是一样的。现在，只选择第一行。稍后，我们将给出一些关于如何选择最简单的计算方法的建议。我们选择示例矩阵A的第一行，圈出1 5 3。一般来说，圈出11

a12

a13

。

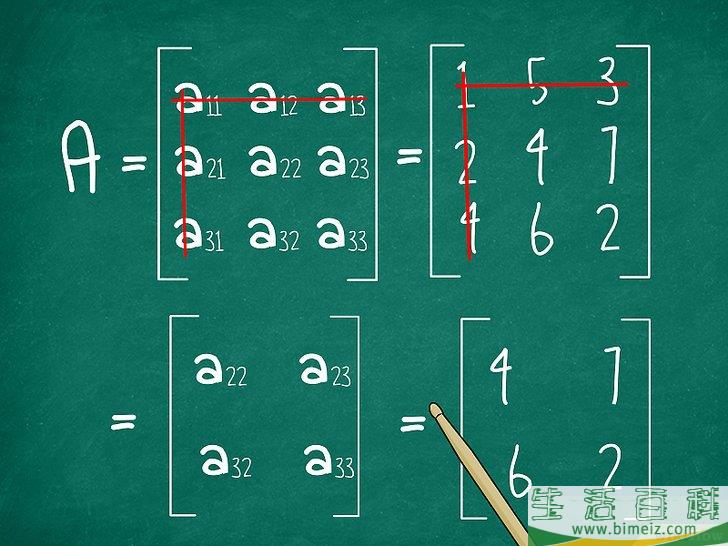
3划掉第一个元素的行和列。

查看圈出的行或列，并选择第一个元素。通过它的行和列画线。剩下四个数字。我们把它看成一个2×2矩阵。在本例中，引用行是1 5 3。第一个元素

在第1行和第1列。划掉第一行和第一列。把剩下的元素写成2×2矩阵

：

 1 

5 3

 2 

4 1

 4 

6 2

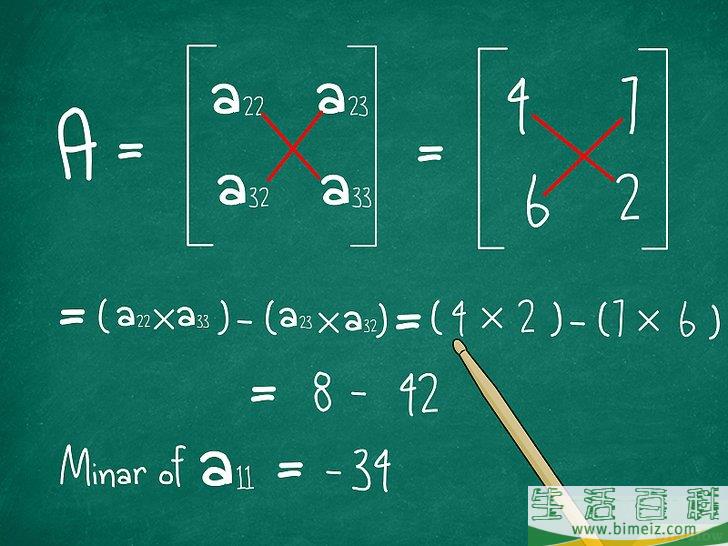
4求出2x2矩阵的行列式。

记住，这个矩阵(

a

b

c

d

)

{\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}

5将结果乘以你选择的元素。

记住，当你决定划去哪一行和哪一列时，是从引用行（或列）中选择了一个元素。将这个元素乘以刚刚计算出的2x2矩阵的行列式。在本例中，我们选择了a11

，值为1。将它乘以-34（2x2矩阵的行列式），得到1*-34 =

-34

。

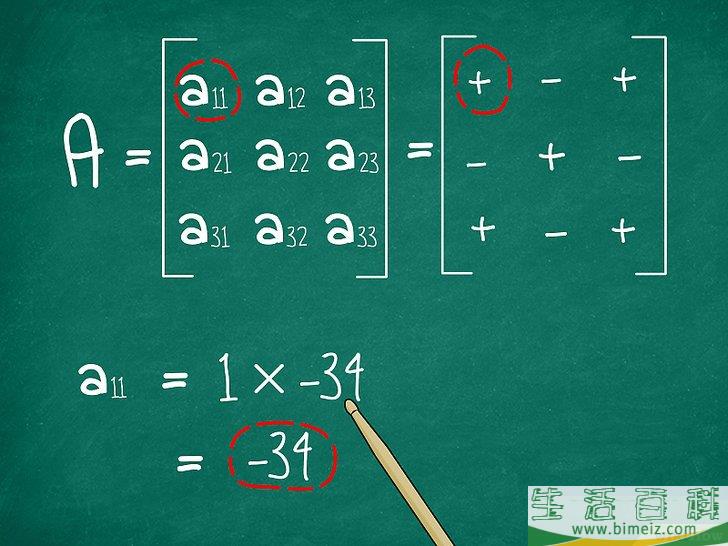
6确定答案的正负号。

接下来，将答案乘以1或-1来得到所选元素的

代数余子式

。你用哪一个取决于元素在3x3矩阵中的位置。记住这个简单的正负号图来找出哪个元素是正，哪个元素是负：+

- +

- + -

+ - +

由于我们选择了a11

，用a +标记，将结果乘以1。（也就是说，不用管它）。答案还是

-34

。

或者，你可以用公式(-1)来计算正负号，其中i

和j

是该元素的行数和列数。

7对引用行或列中的第二个元素重复这个过程。

返回到初始的3x3矩阵，包含你之前圈出的行或列。对这个元素重复相同的过程：

划掉这个元素所在的行和列。

在本例中，选择元素a12

（值为5）。划掉第一行（1 5 3）和第二列(

5

4

6

)

{\displaystyle {\begin{pmatrix}5\\4\\6\end{pmatrix}}}

8对于三个元素重复这个操作。

你还要找出一个余子式。计算引用行或列中第三项的i。在本例中，下面是计算a13

余子式的简要描述：划掉第1行和第3列，得到(

2

4

4

6

)

{\displaystyle {\begin{pmatrix}2&4\\4&6\end{pmatrix}}}

9将三个结果加起来。

这是最后一步。你已经算出来三个代数余子式，每个分别对应单行或单列中的每个元素。把它们加起来，你就得到了3x3矩阵的行列式。在本例中，行列式为

-34

+

120

+

-12

=

74

。

广告

方法2方法2 的 2:简化问题

1选择0最多的引用行或列。

记住，你可以选择任意

行或列作为引用。不管你选哪一个，结果都是一样的。如果你选择一个带有零的行或列，只需要计算非零元素的代数余子式。原因如下：假设你选择第2行，包含元素a21

、a22

和23

。要解决这个问题，我们要看三个不同的2x2矩阵。我们把它们叫做A21

、A22

和A23

。

3x3矩阵的行列式是a21

|A21

| - a22

|A22

| + a23

|A23

|。

如果a22

和a23

都为0，公式就变成a21

|A21

| - 0*|A22

| + 0*|A23

| = a21

|A21

| - 0 + 0 = a21

|A21

|。现在我们只需计算一个元素的代数余子式。

2利用行加法使矩阵更简单。

如果你把一行的值加到另一行，矩阵的行列式不变。列也是如此。你可以重复这样操作，或者在加之前将值乘以一个常数，从而使矩阵有尽可能多的0。这样可以节省很多时间。例如，假设你有一个3×3的矩阵：(

9

−

1

2

3

1

7

5

−

2

)

{\displaystyle {\begin{pmatrix}9&-1&2\\3&1&0\\7&5&-2\end{pmatrix}}}

3学习三角矩阵的快捷方法。

在这些特殊情况下，行列式就是主对角线上的元素的乘积，从左上角的a11

到右下角的a33

。我们讨论的仍然是3x3矩阵，但是“三角”矩阵有非零

值的特殊模式：上三角矩阵：所有非零元素都在主对角线上或主对角线之上。下面全部是0。

下三角矩阵：所有非零元素都在主对角上或主对角之下。

对角矩阵：所有非零元素都在主对角上。（上述矩阵的一个子集）

广告

注意事项

如果有一行或列的所有元素都是0，那么这个矩阵的行列式就是0。

这种方法可以扩展到任何大小的方阵。例如，如果将这种方法用于4x4矩阵，“划掉”后将得到一个3x3矩阵，你可以按照上面的描述计算行列式。但是提醒一句，手动计算非常繁琐！

广告

jiaoyu/11941.html

以上就是矩阵,行列式,元素的相关信息资料了，希望能帮到您。